Arşimet Prensibi (Suyun Kaldırma Kuvveti)
Arşimet Prensibi, sıvı dolu olan bir kaba daldırılmış cismin hacminin, taşan sıvının hacmi ile doğru orantılı olmasını ifade eder.
Arşimet Prensibi Nedir?
Bu cismin ağırlık merkezinden geçen düşey bir kuvvetle yukarı doğru itilir. Bu itme kuvveti “Suyun kaldırma kuvveti” olarak adlandırıldığı gibi “Arşimet Prensibi” olarak da adlandırılmaktadır.
Arşimet Prensibi’ne dayalı olarak kullanılan temel formüller şunlardır:
- Kaldırma kuvveti (Fk) ➡️ Fk = dsıvı * Vb * g
- Fk, kaldırma kuvvetini temsil eder.
- dsıvı, sıvının yoğunluğunu temsil eder (kg/m³).
- Vb, cismin sıvı içinde yerinden aldığı hacmi temsil eder (m³).
- g, yerçekimi ivmesini temsil eder (m/s²).
- Cismin batan ağırlığı (Gb) ➡️ Gb = G – Fk
- Gb, cismin sıvı içindeki etkin, batan ağırlığını temsil eder.
- G, cismin gerçek ağırlığını temsil eder (N, Newton cinsinden).
- Fk, kaldırma kuvvetini temsil eder (N, Newton cinsinden)
Arşimet prensibinde kullanılan formüller, cismin sıvı içinde yüzmesi, sıvı içinde gömülü olup batmaması ve batması şeklinde özetlenmesi aşağıdaki görsel üzerinden daha anlaşılır bir şekilde gösterilmiştir.
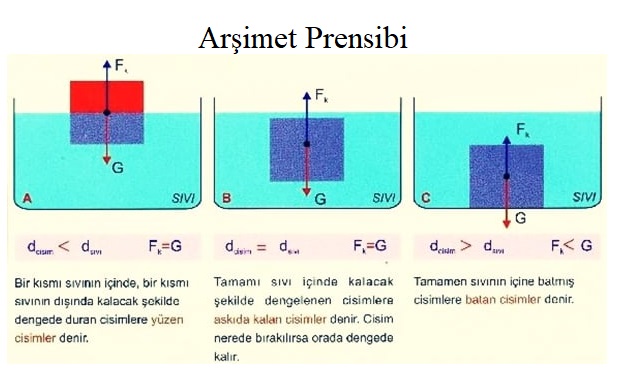
⭐ Yüzen cisimler
dcisim < dsıvı
Fk = Gb
Vb*dsıvı*g = Vc*dcisim*g
⭐ Askıda kalan cisimler
dcisim = dsıvı
Fk = Gb
Vb*dsıvı*g = Vc*dcisim*g
⭐ Batan cisimler
dcisim > dsıvı
Fk < Gb
Vb*dsıvı*g < Vc*dcisim*g
Arşimet Prensibi ile ilgili örnek bir soru ve çözümü aşağıda verilmiştir.
❓ Hacmi 0,5 m³ olan bir cisim, yoğunluğu 1000 kg/m³ olan suya daldırılıyor. Cismin yoğunluğu 800 kg/m³ olsun. Bu durumda cismin üzerine etkiyen kaldırma kuvvetini ve su içindeki etkin ağırlığını hesaplayınız. (g = 9,81 m/s²)
- ❗ İlk olarak, kaldırma kuvvetini (Fb) hesaplamalıyız.
- Fb = ρ * V * g
- Soruda bize, ρ (suyun yoğunluğu) = 1000 kg/m³, V (cismin yerinden aldığı hacim) = 0,5 m³ ve g (yerçekimi ivmesi) = 9,81 m/s² verilmiştir.
- Fb = 1000 kg/m³ * 0,5 m³ * 9,81 m/s² = 4905 N
- Bu nedenle, cismin üzerine etkiyen kaldırma kuvveti 4905 N’dir.
- ❗ Sıra geldi cismin su içindeki etkin ağırlığını (We) hesaplamaya. İlk olarak cismin gerçek ağırlığını (W) bulmalıyız. Cismin ağırlığı, yoğunluğu (ρ_c) ile hacmi (V) ve yerçekimi ivmesi (g) çarpılarak bulunur.
- W = ρ_c * V * g
- Soruda, ρ_c (cismin yoğunluğu) = 800 kg/m³ olarak verilmiştir.
- W = 800 kg/m³ * 0,5 m³ * 9,81 m/s² = 3924 N bulunur.
- We = W – Fb
- We = 3924 N – 4905 N = -981 N bulunur
👍🏻 Etkin ağırlık -981 N olarak bulunmuştur. Negatif değer, cismin yukarı doğru bir kuvvetle itildiğini gösterir. Yani bu demektir ki cisim su içinde yüzmektedir.
Arşimet Prensibi, sıvılar içindeki kaldırma kuvvetini anlamak, cisimlerin batma veya yüzme durumunu belirlemek ve hidrostatik denge gibi uygulamalar için kullanılmaktadır.
Arşimet Prensibi’nin Ardındaki Hikaye
Rivayete göre, Sicilya’da kuyumcuların altın diye sattıkları malların içine yapım aşamasında daha değersiz metaller katarak haksız kazanç sağladıklarına dair dedikodular Hükümdar Hieron’un kulalağına kadar gelir.
Hikayeye göre Arşimet, düzensiz şekilli nesnelerin hacmini ölçmenin bir yolunu arıyordu çünkü Syracuse Kralı Elieron, kuyumcunun yeni altın çelengine gizlice bazı metaller eklediğinden şüpheleniyordu ve Arşimet’e bunu çözmesini emretmişti.
Ne yapıp ettiyse bu sorunu nasıl çözeceğini bir türlü bulamayan Arşimet, Sade bedeni değil aynı zamanda yorgun zihnini de dinlendirmek üzere banyo yapmaya hamama gider ve bedenini içi sulu dolu olan küvetin içine bırakır.
Bu sırada dışarıya suyun taştığını gören Arşimet, aklından çıkmayan problemin çözümsüzlüğüyle dalgın dalgın taşan suya bakarken kendini biraz daha suya batırır. Daha çok suyun dışarı taştığını fark eden Arşimet, taşan su ile kendi vücut ağırlığı arasında bir bağlantı olabileceği fikri kafasına dank eder.
Bir başka deyişle taşan suyun hacmi içine konan kütlenin hacmiyle doğru orantılıdır. Şüphesiz hamama gelmeden önce Arşimet’in aklında böylesi bir deney yapmak yoktu; ancak kurnanın içindeki tas Arşimet’in ilham kaynağı olmuş, daha önce aklına gelmemiş olan bu parlak fikrin heyecanı içinde küvetin içine farklı cisimler koyar.
Yer değiştiren suyun hacmi ile banyo küvetine koyduğu her şeyin hacminin tam olarak eşit çıktığını görür. Bunun üzerine Arşimet, Yunanca ‘Buldum‘ anlamına gelen ‘Eureka, Eureka, Eureka!‘ nidalarıyla anadan üryan bir halde ve çevredekilerin şaşkın bakışları arasında kendisini şehrin sokaklarına atmıştır.
Arşimet’in uğruna hamamdan çırılçıplak fırladığı buluşu cisimlerin gerçek hacimlerini belirlemede kullanılabilecek bir ölçme yönteminin ilk denemesidir.
Arşimet’in bulduğu şey; su içine daldırılan bir cismin taşırdığı suyun ağırlığı kadar ağırlığını kaybetmesi ilkesine dayanmaktaydı.
Arşimet, altın çelenk ile aynı kütledeki saf altının (eğer aynı madde iseler yoğunlukları aynı olması gerekir) taşıracakları su miktarlarının aynı olması gerektiğini ileri sürmüştür. Ardından, çelengi suya daldırır ve taşırdığı su miktarını ölçer.
Daha sonra aynı ağırlıktaki saf altını suya sokar, daha az miktarda su taşırdığını ölçer. Böylece kralın ısmarladığı çelengin saf altından yapılmadığını ortaya çıkarmıştır.
Kaynak: https://www.sciencedirect.com/topics/engineering/archimedes-principle
